PID算法的FPGA实现

PID算法的FPGA实现

　　3.2 乘积和求和模块

　　通过误差计算模块求出e(k)、e(k-1)、e(k-2)后，由公式(5)知，要计算出控制量还必须将其分别与乘积因子做乘法运算，通过硬件描述语言来实现乘法运算的功能：

　　按照上述程序，在Quartus II完成编译后，其仿真结果如图4所示。

图4 乘法器仿真图

　　现在可计算出α0e(k)、α1e(k-1)、α2e(k-2)三个乘积项的计算结果，将上面三个乘积项求和就可以得出控制量△u(k)。程序代码如下所示，其中输入val0[15..0]、val1[15..0]、val2[15..0] 分别对应α0e(k)、α1e(k-1) 、α2e(k-2)乘积的结果，输出val[15..0]就是控制量△u(k)的值。

　　按照上述程序，在Quartus II完成编译后，其仿真结果如图5所示。

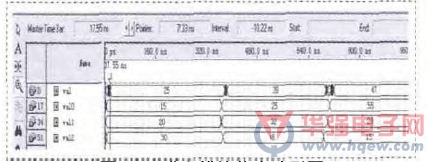
图5 PID求和模块仿真波形图

　　3.3 温度检测及输出控制电路设计

　　本文用到的温度测量器件是K型热电偶，温度测量范围为0～1200℃。热电偶输出的是模拟电压信号，必须进行A/D转换，同时还需对热电偶进行冷端补偿和非线形校正。为了解决上面的问题，本文采用的是K型热电偶专用数字转换器MAX6675芯片，MAX6675芯片内部集成了热电偶放大器，内置高达12位的模数转换器。还包括了非线性矫正、冷端补偿、断线检测等功能模块。MAX6675的工作温度范围为-20～85℃，温度的测量范围为0～1024℃，温度分辨率可以达到0.25℃。假设D为A/D转换后得到的数字量对应的十进制数值，那么测量温度值T可以通过如下公式算出：

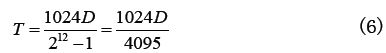
　　输出控制电路采用的是PWM(脉宽调制)方式，实现对电阻炉的温度控制。光耦芯片选用MOC3061，用于对强弱电路的隔离，双向导通可控硅选用的是BT137_600E。如果占空比越高，那么相对可控硅导通的时间也就越长，电阻炉加热温度也就越高，反之温度也就会慢慢散热降低，从而达到控制炉温的目的。

　　4.结语

　　本文分析了PID算法，给出了在FPGA内部硬件实现增量式PID控制的主要设计思路。在电阻炉为控制对象的温控系统中，系统工作稳定，在整个过程没有出现震荡和较大波动，并且温度控制精度在始终保持在5%以内;系统的抗干扰能力增强，对现场的各种噪声和干扰具有较好的抑制作用。

关注电子行业精彩资讯，关注华强资讯官方微信，精华内容抢鲜读，还有机会获赠全年杂志。

关注方法：添加好友→搜索“华强微电子”→关注

或微信“扫一扫”二维码